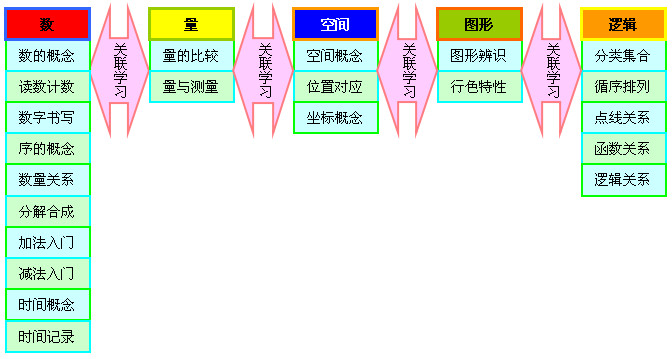
1）多元呈现的关联学习

五大学习内容，分成22个多元领域，实现课程的关联互动学习。

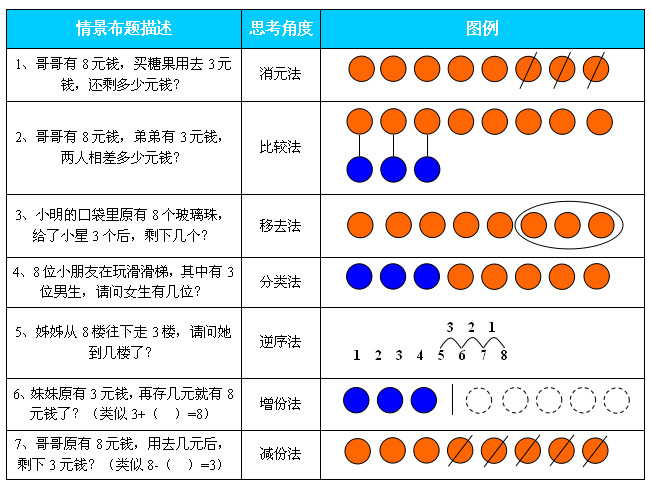
2）多模式情景布题

多模式的两个方面：题型模式（同一解答方式的各种题型变化）

解答模式（同一题型的多种解答方式选择）

生活化的题型模式编辑，让孩童了解不一样题型描述但其数学解答确是一样的。从而明了万变不离其中的道理。

多方法的解答模式编辑，训练孩童从不同的角度来思考问题，拓宽思路，把复杂问题转化为简单问题，从已知的解答方法中找到适合（理解与认同）自己的方式来解决问题。使其在处理复杂问题是具有灵活变通的基础，实现解决问题的能力提升。同时也是对问题的一种验证手段。

范例一：有那些事例可用8-3=( 　　)来解答？可从那些思考角度来解答？

范例二：当孩童在遇到12 – 8这种需要借位的减法时，也有多模式的概念。

模式一：补数法

        13 － 8 

　　　　＝ 3 ＋ 2

　　　　＝ 5

模式二：分解（连减）法

        13 － 8 

　　　　＝13 － 3 － 5

　　　　＝10 － 5

　　　　＝ 5

模式三：分解法

        13 － 8 

　　　　＝10 ＋ 3 － 3 － 5

　　　　＝10 － 5

　　　　＝ 5

模式四：运算法

        13 － 8 ＝ 5

              13

           －  8

        ―――――

               5

模式五：分解运算法（对于减数是两位的最好）

        13 － 8 ＝ 5

　　　　10 ＋ 3

　　　　－   8

　　　　―――――――

　　　　2 ＋ 3 ＝ 5

3）多步骤的演算过程

通过对多步骤演算过程的训练，让孩童在处理复杂问题时能够逐步分拆问题，把复杂的问题简化成较容易的多个问题（步骤）来完成，避免犯简单思维（单一步骤）的毛病。

例1：姐妹两去逛超市，姐姐用了5元钱，比妹妹多用了3元钱，姐妹两一共用了多少元钱？这是一道加减混合的应用题，当题目当中出现“一共”时，孩童往往会根据以往的经验来判定是简单的加法练习，很自然就作出了5 ＋ 3 ＝ 8 的答案了。

而实际的做法是：

步骤一：姐姐用的钱  5（元）

步骤二：妹妹用的钱  5 － 3 ＝ 2（元）

步骤三：一共用的钱  5 ＋ 2 ＝ 7（元）

例2：弟弟有2元钱，哥哥有5元钱，哥哥给弟弟1元钱后，两人共有多少元钱？

方法一：

步骤一：弟弟得到1 元后的钱    2 ＋ 1 ＝ 3（元）

步骤二：哥哥给出 1 元后的钱    5 － 1 ＝ 4（元）

步骤三：兄弟两一共有的钱       3 ＋ 4 ＝ 7（元）

方法二：同一个集合，数量守恒

步骤一：兄弟两一共有的钱     5 ＋ 2 ＝ 7（元）

我们把“例1”加大难度，

例3：姐妹两去逛超市，姐姐有5元钱，用了3 元钱，比妹妹少用了1元钱，妹妹却把钱用完了，姐妹两一共用了多少元钱？一共又有多少元钱？

问题1：

步骤一：姐姐用的钱  3（元）

步骤二：妹妹用的钱  3 ＋ 1 ＝ 4（元）

步骤三：一共用的钱  3 ＋ 4 ＝ 7（元）

问题2：

步骤一：姐姐有的钱   5（元）

步骤二：妹妹有的钱   4（元）

步骤三：一共有的钱   5 ＋ 4 ＝ 9（元）

问题1和问题2的有效步骤：

步骤一：妹妹用的钱  3 ＋ 1 ＝ 4（元）

步骤二：一共用的钱  3 ＋ 4 ＝ 7（元）

步骤三：一共有的钱  5 ＋ 4 ＝ 9（元）